计算机数学应该从娃娃抓起。本文作者曾在7岁和8岁儿童课堂和孩子一起互动,学习图论的基本知识,向她们传递了数学之美,非常有意思!
我的女儿上小学三年级。今天早上,我被邀请到她们的数学课堂,和那些8、9岁充满好奇的孩子们做了一次精彩的数学互动。
我的目的是想让这群孩子自己主动的愉快的发现在拓扑学中的欧拉公式。
一开始,我举了一个简单的例子,画了一张各边连接起来的平面图。
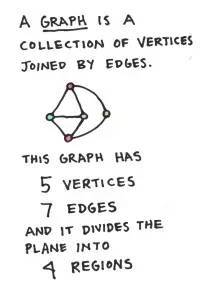
我要她们数一数图中顶点(Vertices)、边数(Edges)和这个图分割出来的区域个数(Regions),并且强调“外部区域”也应该算区域之一(比如一个圆把平面分割为两个区域)。
然后我神秘的告诉她们,欧拉曾经计算过V−E+R,结果发现了一个惊人的秘密,看看她们能不能发现?
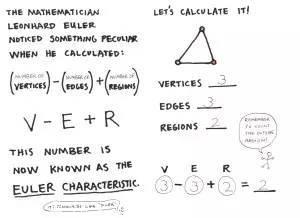
我事先给这些小朋友们每人准备一些图册,里面有一些不同的用来计算欧拉公式的平面图。
现在,我让她们自己来计算。
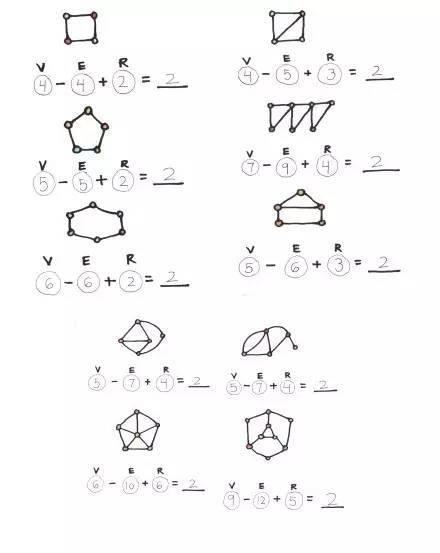
后来,每个小朋友都发现了这个秘密,她们惊呼,为什么我们得出的结果都等于2呢? 惊讶之余,她们已经被这个神奇的结果深深吸引!
现场的老师也感到非常好奇,其中一个惊奇的问我,为什么它们的结果都等于2呢?
显然,已经吊足了孩子们的胃口。现在,我建议她们去尝试计算一些不同的平面图,看看结果是不是还等于2?
不过,和前次不同的是,这次我要求孩子们自己画图,然后自己计算。
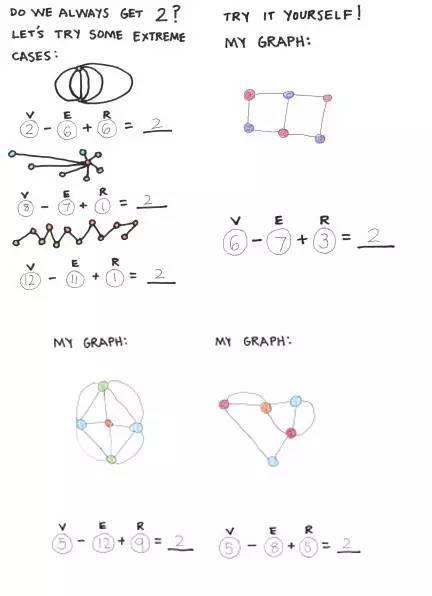
等孩子自己画完和计算完,我还告诉了她们一些特殊的例子,比如,没有闭环连接的图形,或边交叉的图形等等。像下面这样:
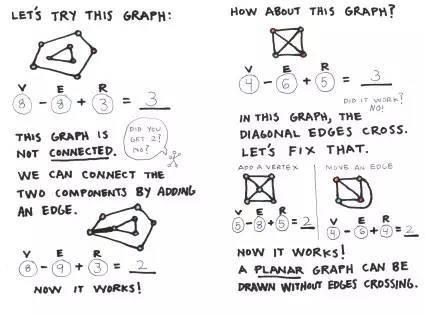
当然,结果同样等于2。
现在,孩子们都瞪着双眼期待我来解释这到底是为什么? 说实话,刚开始,我原本打算游戏就到此为止,不想给出证明,毕竟,她们都是8、9岁的孩子,对于一个三年级的孩子来说,确实太难了点。可是,现场的老师也开始强烈要求我解释一下为什么,他们说,即使那些孩子听不懂,让她们大概了解一下也没关系。
好吧,我是这样解释的。
我们得从最开始说起。当只有一个顶点,没有边的时候,欧拉公式也是成立的。如下图:

然后,你在图上加一个顶点,再将两个顶点连接起来,同样,也是成立的。因为这时多了一个顶点,同时也多了一个边,V-E,2的结果依然成立。
同样,如果在一个区域里面画一条边,将这个区域分裂成两个区域后,因为此时多了一条边,同时也多了一个区域,-E+R,2的结果同样保持。
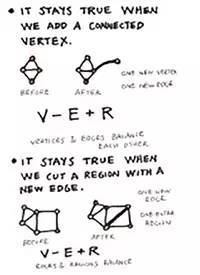
是的,不管你加多少边,画多少顶点,这个等式都能保持平衡。

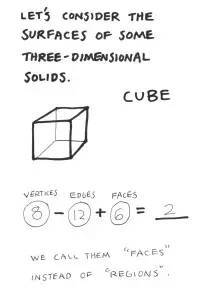
现在,我们来看看三维立体图和它们的面。
对于不同的多面体,V-E+R=2都成立。 不同的是,在计算多面体时,我们用多面体的面(Face)来代替平面图的区域(Region)。
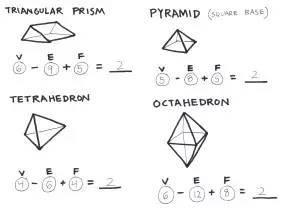
现在,我再让孩子们自己画立体图,然后自己来计算欧拉公式。
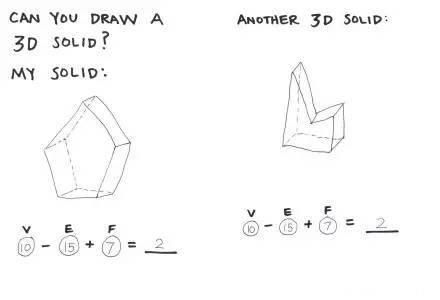
我开始教她们怎样画一个立体方块和其它各种立体图形。我原本以为,对于三年级的孩子来说,画出这些立体图形会比较困难,不过,很多孩子画得非常好。
本文所用的图就是其中一个孩子画的。
后来,所有的孩子都带了一本自己的画册回家,上面有许多平面图和立体图。
What a great day!
说几句欧拉:
Leonard Euler出生于瑞士,长期在德国和俄罗斯工作。由于欧拉的巨大成就,三个国家一直都声称欧拉是本国数学家,嘴仗没少打。

这是瑞士法郎上的欧拉。印上钞票的数学家只有两位,大家猜猜另一位是谁。

德国邮票上的欧拉。边上写着欧拉公式。

苏联邮票上的欧拉。他的一只眼睛长期失明。
欧拉巨大的创作性鲜有匹敌。他是历史上所有数学家中最高产的一位。
∑编辑 | Gemini